没看过第一期的可以点击这个地址:http://bns.17173.com/news/09042014/161706404_1.shtml
好了这期说说吐槽大家提出的一些问题,很让人郁闷的问题。
Q1:当暴击数值在9200~9300时,会接近之前推出函数的顶峰,之后下降。
A1:由于样本数量不够多,加之函数是一个偶次函数,偶次函数在某个区间内会有极值,属于正常现象。
当然了为了弥补这个问题,咨询过部分其他游戏的数据帝,和一些游戏开发者后,对研究方向做出一定调整,望修复问题。
修复内容:
自变量修正为暴击数值的倒数。
在修正为倒数后再次进行重新使用高次函数进行拟合,得到的图像与函数为:
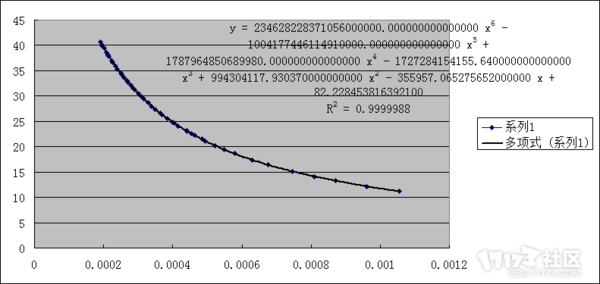
很明显会发现的问题是R^2明显小于之前提出的高次函数拟合(这个明显小于的概念……嗯你们将就着看吧)
但是毕竟是近似拟合,所以不能强求那么多了。
或许这样看数值分析大家不能明白什么,但是在函数本质上发生了变化,而之所以选用高次函数进行拟合,是高次函数在系数非常小或者自变量变化非常小的时候,可以拟合绝大部分的曲线。
但是EXCEL只能拟合最高6次的函数,也是不能推出更精确的公式,表示抱歉和可惜吧。
好了废话不多说,这一次推出的公式可以帮助大家了解,到100%暴击率是不可能这个事实以及……后期暴击成长的幅度是特么的多小。。。
嗯好了具体公式如下:
暴击率为y%,暴击数值为1/x
y = 234628228371056000000*x^6 - 1004177446114910000*x^5 + 1787964850689980*x^4 - 1727284154155.64*x^3 + 994304117.93037*x^2 - 355957.065275652*x + 82.2284538163921
好了最后还是说一句,有问题是肯定的毕竟是推倒,我只希望大家看帖和看新闻的时候能理智点,管住自己的手(zui)。
如果后期暴击计算公式有修改被发现了我会及时推算并发帖告诉大家~当然对此有兴趣的可以PM我来交流下,毕竟数据这东西有时候研究起来是很好玩的,对吧米娜桑~
